Nombre Pi (3,14), noté ∏, bien connu de tous mais mystérieux : Retour sur sa découverte et son calcul…
Pi1 est un nombre, que l’on représente par la lettre grecque du même nom : π. C’est le rapport constant de la circonférence d’un cercle à son diamètre dans un plan euclidien. On peut également le définir comme le rapport de la superficie d’un cercle au carré de son rayon.
Sa valeur approchée par défaut à moins de 0,5×10–15 près2 est 3,141 592 653 589 793 en écriture décimale3,4.
De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques5.
Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine6.
La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
L’usage de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec —, n’est apparu qu’au XVIIIe siècle. Auparavant, sa valeur était désignée par diverses périphrases comme la « constante du cercle » ou son équivalent dans diverses langues.
Dans les dictionnaires et ouvrages généralistes7, π est défini comme le rapport, constant dans le plan usuel qu'est le plan euclidien, entre la circonférence d’un cercle et son diamètre. Ce rapport ne dépend pas du cercle choisi, en particulier de sa taille. En effet, tous les cercles sont semblables et pour passer d’un cercle à un autre il suffit de connaître le rapport de la similitude. Par suite, pour tout réel positif k, si un cercle possède un rayon r (ou un diamètre d = 2r) k fois plus grand qu’un autre, alors son périmètre P sera aussi k fois plus grand, ce qui prouve la constance du rapport
Il s’avère que cette définition géométrique, historiquement la première et très intuitive, n’est pas la plus directe pour les mathématiciens quand ils veulent définir π en toute rigueur. Les ouvrages plus spécialisés9 définissent π par l’analyse réelle à l’aide des fonctions trigonométriques elles-mêmes introduites sans référence à la géométrie (voir plus bas).
Ce dernier expose en 1761, dans son ouvrage Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, un développement en fraction continue généralisée de la fonction tangente. Il en déduit qu'un développement de tan(m/n), avec m et n des nombres entiers non nuls, s’écrit14 :
Avec la notation d'Alfred Pringsheim où :
Au cours du XXe siècle, d’autres démonstrations furent trouvées, celles-ci ne demandant pas de connaissances plus avancées que celle du calcul intégral. L’une d’entre elles, due à Ivan Niven, est très largement connue15,16. Une preuve similaire, version simplifiée de celle de Charles Hermite17,18, avait été trouvée quelque temps auparavant par Mary Cartwright19.
C'est au XIXe siècle que ce résultat est démontré. En 1873, Hermite prouve que la base du logarithme népérien, le nombre e, est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (le théorème d'Hermite-Lindemann) qui stipule que, si x est algébrique et différent de zéro, alors ex est transcendant. Or eiπ est algébrique (puisqu'il est égal à -1). Par contraposition, iπ est transcendant, donc comme i est algébrique, π est transcendant.
Une conséquence importante de la transcendance de π est que celui-ci n'est pas constructible. En effet, le théorème de Wantzel énonce en particulier que tout nombre constructible est algébrique. En raison du fait que les coordonnées de tous les points pouvant se construire à la règle et au compas sont des nombres constructibles, la quadrature du cercle est impossible ; autrement dit, il est impossible de construire, uniquement à la règle et au compas, un carré dont la superficie serait égale à celle d'un cercle donné21.
Alors qu’en 2007, on connaissait déjà plus de 1012 décimales de π23, de nombreuses applications concrètes, comme l’estimation de la circonférence d’un cercle, n’ont besoin que d’une dizaine de chiffres. Par exemple, la représentation décimale de π tronquée à 39 décimales est suffisante pour estimer la circonférence d’un cercle dont les dimensions sont celles de l’univers observable avec une précision comparable à celle du rayon d’un atome d’hydrogène24,25.
Étant donné que π est un nombre irrationnel, sa représentation décimale n’est pas périodique et ne prend pas fin. La séquence des décimales de π a toujours fasciné les mathématiciens professionnels et amateurs, et beaucoup d’efforts ont été mis en œuvre afin d’obtenir de plus en plus de décimales et d’en rechercher certaines propriétés26, comme l'occurrence de nombres premiers dans les concaténations de ses décimales (voir la section d'article Nombre premier issu de troncature de constante.)
Malgré les importants travaux d’analyse effectués et les calculs qui ont réussi à déterminer plus de 200 milliards de décimales de π, aucun modèle simple n’a été trouvé pour décrire la séquence de ces chiffres27. Les chiffres de la représentation décimale de π sont disponibles sur de nombreuses pages web, et il existe des logiciels de calcul des décimales de π qui peuvent en générer des milliards et qu’on peut installer sur un ordinateur personnel.
Par ailleurs, le développement décimal de π ouvre le champ à d’autres questions, notamment celle de savoir si π est un nombre normal, c’est-à-dire que ses chiffres en écriture décimale sont équirépartis. On peut aussi se demander si π est un nombre univers, ce qui signifie qu’on pourrait trouver dans son développement décimal n’importe quelle suite finie de chiffres. En 2006, il n’existait pas de réponse à ces questions28.

Voir ci-dessous pour d’autres approches fractionnaires (Histoire, Approximation numérique, fractions continues et Mémorisation de π).
Archimède a utilisé cette approche en comparant les résultats obtenus par la formule en utilisant deux polygones réguliers ayant le même nombre de côtés, pour lesquels le cercle est pour l’un circonscrit et pour l’autre inscrit. Il a réussi, avec un polygone à 96 côtés, à déterminer30 que 3 + 10/71 < π < 3 + 1/7.
On peut également obtenir des valeurs approchées de π en mettant en œuvre des méthodes plus modernes. La plupart des formules utilisées pour calculer π se basent sur la trigonométrie et le calcul intégral. Cependant, certaines sont particulièrement simples, comme la formule de Leibniz31 :
Cette série converge si lentement que près de 200 termes sont nécessaires pour calculer π avec deux décimales exactes32. Cependant, il est possible de définir une suite similaire qui converge vers π beaucoup plus rapidement, en posant : et en définissant :
et en définissant : 
Le calcul de π10,10 demande alors un temps similaire à celui requis pour calculer les 150 premiers termes de la série initiale, mais la précision est bien meilleure car π10,10 = 3,141592653… approche π avec neuf décimales exactes33. On trouvera plus loin des méthodes de calcul plus élaborées, donnant des convergences bien plus rapides encore.
Découvert en 1855, le papyrus de Rhind contient le texte, copié au XVIe siècle avant notre ère par le scribe égyptien Ahmès,
d'un manuel de problèmes plus ancien encore. On y trouve utilisé
plusieurs fois une méthode pour évaluer l'aire d'un disque en prenant le
carré dont le côté est égal au diamètre du disque diminué d'un
neuvième. Cette méthode conduit à une évaluation de π de 256/81.
Une justification possible de celle-ci s'appuie sur le schéma ci-contre. Si le disque a pour diamètre 9. L'aire du disque est légèrement supérieure à l'aire de l'octogone (irrégulier) obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l'aire du disque est alors évaluée à 64 soit l'aire d'un carré de côté 8. Le rapport entre l'aire du disque et le carré du rayon est alors évalué par 64/(9/2)2, c'est-à-dire 256/8137. Mais l'hypothèse que ce procédé ait conduit à l'approximation du papyrus Rhind ne fait pas l'unanimité chez les historiens.
Vers 700 av. J.-C., le texte indien Shatapatha Brahmana donne une approximation de π : 25/8 (= 3,125) et le Baudhāyana Sulbasūtra en donne deux autres : 900/289 (≈ 3,11) et 1156/361 (≈ 3,20)38. Des calculs d'astronomie ont ensuite conduit à une autre approximation védique : 339/108 (≈ 3,139)39. Au début du VIe siècle ap. J.-C., Aryabhata donne une approximation plus précise : = 3,1416. Comme |π – 3,1416| < 0,0000075, il s'agit d'un résultat remarquable, exact à 10−5 près.
= 3,1416. Comme |π – 3,1416| < 0,0000075, il s'agit d'un résultat remarquable, exact à 10−5 près.
C'est dans le traité d'Archimède (287 à 212 av. J.-C.) intitulé De la mesure du cercle que l'on peut lire une démonstration liant l'aire du disque et l'aire du triangle ayant une base de longueur le périmètre du cercle et pour hauteur le rayon, démontrant ainsi qu'une même constante apparaît dans le rapport entre aire du disque et carré du rayon et entre périmètre et diamètre40.
Cette démonstration s'appuie sur la méthode d'exhaustion et un raisonnement par l'absurde41. En partant d'un carré inscrit dans le cercle et d'un carré circonscrit au cercle et en multipliant indéfiniment par 2 le nombre de côtés, il prouve que l'aire du disque ne peut être inférieure ni supérieure à celle du triangle correspondant.
Dans le même traité40
Archimède établit un encadrement du périmètre du cercle à l'aide des
périmètres des polygones réguliers inscrit et circonscrit au cercle et
possédant 96 côtés42.
Pour calculer les périmètres de ces polygones, il part d'hexagones
inscrits et circonscrits et met en évidence les formules donnant le
périmètre d'un polygone dont le nombre de côtés a doublé. Son calcul
revient à démontrer que 3 + 10/71 < π < 3 + 1/742. La moyenne de ces deux valeurs est d'environ 3,14185. Archimède s'arrête à 96 côtés
car les calculs qu'il est amené à effectuer, avec valeurs approchées,
sont déjà longs pour l'époque. Mais il met en place ainsi une méthode
qui sera reprise par ses successeurs et qui permet en théorie une
précision aussi petite que souhaitée. Il faut cependant une précision
toujours plus grande dans les premiers calculs à chaque fois que l'on
double le nombre de côtés du polygone. Ptolémée, scientifique grec ayant vécu trois siècles après Archimède, donne une valeur de 3,1416, qu'il a probablement obtenue grâce à Apollonius de Perga43[réf. insuffisante].
Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres,
propose comme rapport entre le périmètre et le diamètre la valeur
pratique de 3 mais développe des calculs proches de ceux d'Archimède
mais plus performants et fournit une approximation de π de 3,141644. Le mathématicien chinois Zu Chongzhi donne une approximation rationnelle encore plus précise de π45 : π ≈ 355/113 (dont les développements décimaux sont identiques jusqu'à la 6e décimale, π ≈ 3,141 592 6 et 355/113 ≈ 3,141 592 9) et montre que 3,141 592 6 < π < 3,141 592 746, en utilisant l'algorithme de Liu Hui (en) appliqué à un polygone à 12 288 côtés. Cette valeur demeure la meilleure approximation de π au cours des 900 années qui suivent.
Jusqu’en 1400 environ, la précision des approximations de π n’excédait pas les 10 décimales. Les progrès en matière de calcul intégral et de séries vont permettre d’améliorer cette précision. Les séries permettent d’approcher π avec d’autant plus de précision qu’on utilise de termes de la série pour le calcul. Vers 1400, Madhava de Sangamagrama trouve ce qui constitue, en langage moderne, le développement de la fonction arc tangente (redécouvert par James Gregory et Gottfried Wilhelm Leibniz au XVIIe siècle) :![\arctan(x)=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{2k+1}\quad (x \in \left[-1,1\right]).](https://upload.wikimedia.org/math/7/8/4/784c0a7223978b13c2c8e2cbb361c057.png) Le cas particulier x = 1 est la série de Leibniz mentionnée plus haut — également connue sous le nom de série de Madhava-Leibniz47,48 — dont la convergence est trop lente.
Le cas particulier x = 1 est la série de Leibniz mentionnée plus haut — également connue sous le nom de série de Madhava-Leibniz47,48 — dont la convergence est trop lente.
Le cas particulier x = 1/√3 : converge bien plus vite, ce qui a permis à Madhava de donner une valeur approchée de π de 3,141 592 653 59, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi (Traité de la circonférence), qui a réussi à donner 16 décimales.
converge bien plus vite, ce qui a permis à Madhava de donner une valeur approchée de π de 3,141 592 653 59, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi (Traité de la circonférence), qui a réussi à donner 16 décimales.
La première contribution importante venant d’Europe depuis Archimède a été faite par François Viète, qui en donne douze décimales, avec un encadrement du reste dans son Canon mathématique en 1579. Il est suivi par Adrien Romain, qui donne 15 décimales en 1591, et l’Allemand Ludolph van Ceulen (1540–1610), qui a utilisé la même méthode géométrique afin de donner une estimation de π correcte à 35 décimales près. Il a été si fier de son calcul, qui lui a demandé une grande partie de sa vie, qu’il a fait graver les décimales sur sa pierre tombale49.
Il est immédiatement suivi par Willebrord Snell, son élève, qui trouve des méthodes plus rapides pour obtenir la même approximation. Dans la même période, les méthodes de calcul intégral et de détermination de séries et produits infinis pour des quantités géométriques ont commencé à émerger en Europe. La première formule de ce type est la formule de Viète (en) :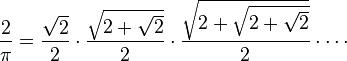
exposée par François Viète en 1579 dans son Canon mathématique et à nouveau[réf. souhaitée] en 1593, dans ses Problèmes variés. Un autre résultat célèbre est le produit de Wallis :
que l’on doit à John Wallis, qui l’a mis en évidence en 1655. Isaac Newton lui-même a utilisé le développement en série de π/6 = arcsin(1/2)50 pour calculer 15 décimales de π ; bien plus tard, il a déclaré : « J’ai honte de vous dire combien de décimales j’ai trouvées grâce à ces calculs, n’ayant aucune autre occupation à l’époque. »51.
En 1706, John Machin a été le premier à trouver 100 décimales de π, en utilisant la formule :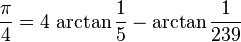 et le développement ci-dessus en série entière de arctan.
et le développement ci-dessus en série entière de arctan.
Les formules de ce type, maintenant connues sous le nom de formules de Machin, ont été utilisées pour battre plusieurs records de décimales connues de π, et demeurent aujourd’hui les formules les plus connues pour calculer π grâce à des ordinateurs. Un record remarquable est détenu par le calculateur prodige Johann Dase qui, en 1844, à l’aide d’une formule de Machin, a calculé de tête 200 décimales de π, à la demande de Gauss. La meilleure valeur obtenue à la fin du XIXe siècle est due à William Shanks, qui a passé quinze ans à calculer 707 décimales de π, bien qu’à cause d’une erreur, seules les 527 premières étaient correctes. De nos jours, il est aisé d’éviter de telles erreurs, en faisant faire les calculs par l’ordinateur, et en utilisant deux formules différentes pour éliminer les risques d’erreur de calcul, de programmation, ou du microprocesseur.
Les avancées théoriques du XVIIIe siècle ont amené les mathématiciens à s’interroger sur la nature de π, notamment sur l’absence de motifs périodiques dans ses décimales, une hypothèse raisonnable au vu des calculs numériques, mais pour laquelle il fallait une approche radicalement différente pour la prouver rigoureusement. Ce tour de force a été réalisé par Johann Heinrich Lambert en 1761, qui fut ainsi le premier à prouver l’irrationalité de π, par la suite Adrien-Marie Legendre a aussi prouvé que π2 aussi était irrationnel. Cette constante (π2) jouait un rôle notable en mathématique, puisqu’elle apparaissait dans la solution du problème de Bâle, qui consistait à trouver la valeur exacte de qui est π2/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.
qui est π2/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.
À partir du XVIIe siècle certains mathématiciens utilisent la notation π/δ où π désigne la circonférence et δ le diamètre53. Le premier à utiliser simplement π est William Jones52 dans son livre Synopsis palmariorum mathesios publié en 1706, à propos du calcul astucieux de ce nombre par la série de son ami Machin. Les mathématiciens continuent cependant d’utiliser d’autres notations. Parmi ceux-ci Euler se met à la notation de Jones54 dans sa correspondance à partir de 1736. Il l’adopte dans son livre Introductio in analysin infinitorum publié en 1748, ce qui eut certainement une grande influence. La notation finit par s’imposer vers la fin du XVIIIe siècle55.
En 1949, à l’aide de l’ENIAC, John von Neumann a obtenu 2037 décimales de π, à la suite d'un calcul qui a duré 70 heures56,57. Des milliers de décimales supplémentaires ont été trouvées au cours des décennies suivantes, l’étape du million de chiffres ayant été passée en 1973. Les progrès n’ont pas seulement été dus aux ordinateurs de plus en plus rapides, mais aussi aux nouveaux algorithmes utilisés. L’une des avancées les plus significatives a été la découverte de la transformée de Fourier rapide dans les années 1960, qui a permis aux ordinateurs de manipuler rapidement de très grands nombres.
Au début du XXe siècle, le mathématicien indien Srinivasa Ramanujan a trouvé de nombreuses nouvelles formules faisant intervenir π ; certaines d’entre elles sont remarquables par leur élégance et leur profondeur mathématique58. L’une de ces formules est la série suivante :
La formule ci-dessous, possédant un lien étroit avec celle énoncée ci-dessus, a été découverte par David et Gregory Chudnovsky en 1987 :
Cette formule donne 14 nouvelles décimales de π à chaque terme58. Vers la fin des années 1980, les frères Chudnovsky l’ont utilisée pour battre plusieurs records de décimales de π calculées. Elle demeure la formule la plus utilisée pour calculer π sur des ordinateurs personnels.
Alors que les séries permettent d’obtenir des valeurs approchées de π
avec un taux de précision supplémentaire à chaque terme qui est
constant, il existe des algorithmes itératifs qui multiplient le nombre
de décimales correctes à chaque étape, avec cependant l’inconvénient que
chaque étape demande généralement un calcul « coûteux ». Une grande
avancée a eu lieu en 1975 lorsque Richard Brent et Eugene Salamin ont
découvert indépendamment la formule de Brent-Salamin, qui double le nombre de décimales correctes à chaque étape59. Il s’appuie sur un vieux résultat pressenti puis démontré par Gauss. En 1818, celui-ci démontre le lien existant entre la moyenne arithmético-géométrique M(1, √2) de 1 et √2 — la longueur de la lemniscate de Bernoulli — et π. La longueur de la lemniscate est  où r représente la distance OA entre le centre et un sommet de la lemniscate et où
où r représente la distance OA entre le centre et un sommet de la lemniscate et où 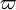 est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1, √2) alors :
est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1, √2) alors :  Salamin et Brent ont utilisé ce résultat pour construire l’algorithme
qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √260.
Salamin et Brent ont utilisé ce résultat pour construire l’algorithme
qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √260.
L’algorithme consiste à poser : , puis à définir les relations de récurrence suivantes :
, puis à définir les relations de récurrence suivantes : 
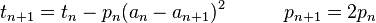 et enfin à calculer ces termes jusqu’à ce que an et bn soient assez proches. On a alors une valeur approchée de π donnée par :
et enfin à calculer ces termes jusqu’à ce que an et bn soient assez proches. On a alors une valeur approchée de π donnée par : 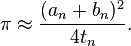
En utilisant cet algorithme, seuls 25 termes sont nécessaires pour calculer 45 millions de décimales. Un algorithme similaire qui quadruple la précision à chaque étape a été trouvé par Jonathan et Peter Borwein61. C’est grâce à ces méthodes qu’en 1999, Yasumasa Kanada et son équipe ont battu le record du nombre de décimales de π qui datait de 1980, en atteignant les 206 158 430 000 chiffres.
En 1997, la formule BBP, découverte par Simon Plouffe, a fait de nouveau progresser la connaissance de π62. La formule,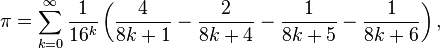 est remarquable car elle permet de calculer n’importe quel chiffre de l’écriture de π en base hexadécimale ou binaire, sans calculer les précédents62. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000e chiffre en binaire de π, qui s’est révélé être 063.
est remarquable car elle permet de calculer n’importe quel chiffre de l’écriture de π en base hexadécimale ou binaire, sans calculer les précédents62. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000e chiffre en binaire de π, qui s’est révélé être 063.
Si une formule de la forme : était trouvée, avec b et c des entiers positifs et p et q
des polynômes de degrés fixés à coefficients entiers (comme pour la
formule BBP ci-dessus), ce serait l’un des moyens les plus efficaces
pour calculer n’importe quel chiffre dans l’écriture de π en base bc sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé[pas clair] et du degré des polynômes.
était trouvée, avec b et c des entiers positifs et p et q
des polynômes de degrés fixés à coefficients entiers (comme pour la
formule BBP ci-dessus), ce serait l’un des moyens les plus efficaces
pour calculer n’importe quel chiffre dans l’écriture de π en base bc sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé[pas clair] et du degré des polynômes.
En 2006, Simon Plouffe a trouvé plusieurs formules faisant intervenir π64. En posant q = eπ (constante de Gelfond), on a :
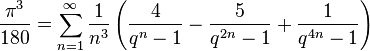 ainsi que :
ainsi que :  où k est un nombre impair, et a, b, c sont des nombres rationnels.
où k est un nombre impair, et a, b, c sont des nombres rationnels.
En août 2010, le record est à nouveau battu par deux informaticiens (un japonais et un américain) avec 5 000 milliards de décimales65.
Le 8 octobre 2014, le nouveau record est 13 300 milliards de décimales66.
π se retrouve aussi dans le calcul des surfaces et volumes des hypersphères (à plus de trois dimensions).
Un nombre complexe z peut s’exprimer en coordonnées polaires de la façon suivante : 
L’apparition fréquente de π en analyse complexe a pour origine le comportement de la fonction exponentielle complexe, décrite par la formule d’Euler : où i est l’unité imaginaire satisfaisant la relation i2 = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360° = 2π rad. En particulier, une rotation de 180° = π rad donne l’identité d'Euler
où i est l’unité imaginaire satisfaisant la relation i2 = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360° = 2π rad. En particulier, une rotation de 180° = π rad donne l’identité d'Euler 
Cette formule a été qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l’addition, la multiplication, l’exponentiation, l’égalité et les constantes remarquables 0, 1, e, i et π67.

Les deux suites définies par sn = n sin(π/n) et tn = n tan(π/n), n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi, on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes s2n et t2n ou encore s3.2n et t3.2n, à l’aide des identités trigonométriques usuelles : (voir pour t2n identité trigonométrique#Formules d'angle moitié -- seconde formule, et pour s2n, 2sin2 α/2 = sin α tan α/2 qui se déduit de identité trigonométrique#Formules d'angle double -- première formule).
(voir pour t2n identité trigonométrique#Formules d'angle moitié -- seconde formule, et pour s2n, 2sin2 α/2 = sin α tan α/2 qui se déduit de identité trigonométrique#Formules d'angle double -- première formule).
En utilisant directement les identités trigonométriques 2sin(x/2) = √2 – 2cos(x) et 2cos(x/2) = √2 + 2cos(x) (x ∈ [0, π]), on peut exprimer s2k+1 et s3×2k (pour k ≥ 1), puis π (par passage à la limite) sous forme de formules où s’emboîtent des racines carrées : (k est le nombre de racines carrées) ou encore :
(k est le nombre de racines carrées) ou encore :  Les deux formules trigonométriques se démontrent simplement géométriquement par le théorème de Pythagore, aussi le même raisonnement peut-il se faire directement sur les suites sn et tn vues comme demi-périmètres de polygones réguliers, sans référence à la trigonométrie.
Les deux formules trigonométriques se démontrent simplement géométriquement par le théorème de Pythagore, aussi le même raisonnement peut-il se faire directement sur les suites sn et tn vues comme demi-périmètres de polygones réguliers, sans référence à la trigonométrie.
Une autre expression de s2k+1, qui peut se déduire simplement de la première de ces deux égalités (multiplier par √2+√…), conduit au produit infini suivant (formule de François Viète, 1593) :
Soient trois suites ,
,  et
et  se définissant mutuellement :
se définissant mutuellement :  ; on a :
; on a : 
Le nombre de décimales correctes (en base 10) double presque à chaque itération.
 ). La suite (xn) quitte l’intervalle [0, 1] et diverge pour quasiment toutes les valeurs initiales.
). La suite (xn) quitte l’intervalle [0, 1] et diverge pour quasiment toutes les valeurs initiales.
On a pour presque toutes les valeurs initiales x0.
pour presque toutes les valeurs initiales x0.

D’autre part, il existe diverses expériences probabilistes où π intervient dans la probabilité théorique. Elles peuvent donc servir, en effectuant un grand nombre d’épreuves, à déterminer une approximation de π.
L’aiguille de Buffon est une expérience de probabilité proposée par Georges-Louis Leclerc, comte de Buffon et consistant à calculer la probabilité qu’une aiguille de longueur a, lancée sur une parquet fait de lattes de largeur L, soit à cheval sur deux lattes, cette probabilité p est72 : même si l'aiguille est courbe73,74.
même si l'aiguille est courbe73,74.
Cette formule peut être utilisée pour déterminer une valeur approchée de π : où n est le nombre d’aiguilles lancées, et x celui d’aiguilles qui sont sur deux lattes à la fois.
où n est le nombre d’aiguilles lancées, et x celui d’aiguilles qui sont sur deux lattes à la fois.
Cette méthode présente rapidement ses limites ; bien que le résultat soit mathématiquement correct, il ne peut pas être utilisé pour déterminer plus que quelques décimales de π expérimentalement. Pour obtenir seulement une valeur approchée de 3,14, il est nécessaire d’effectuer des millions de lancers72, et le nombre de lancers nécessaires croît exponentiellement avec le nombre de décimales voulu. De plus, une très faible erreur dans la mesure des longueurs L et a va se répercuter de façon importante sur la valeur trouvée de π. Par exemple, une différence de mesure d’un seul atome sur une aiguille de longueur de 10 centimètres va se retrouver dès la neuvième décimale de π. En pratique, les cas où l’aiguille semble toucher exactement la limite entre deux lattes va accroître l’imprécision de l’expérience, de sorte que les erreurs apparaîtront bien avant la neuvième décimale.
La méthode de Monte Carlo75 est une autre expérience probabiliste qui consiste à prendre au hasard un point dans un carré de côté 1, la probabilité que ce point soit dans le quart de disque de rayon 1 étant de π/4 ; ceci peut facilement se comprendre étant donné que la superficie de ce quart de cercle est π/4 alors que la superficie du carré est 1.
Par conséquent, les calculs numériques doivent utiliser des approximations de π.
La première approximation numérique de π fut certainement 342. Dans les cas où une situation ne demande que peu de précision, cette valeur peut servir d’approximation convenable. Si 3 est une estimation par défaut, c’est parce qu’il est le rapport entre le périmètre d’un hexagone régulier inscrit dans un cercle et le diamètre de ce cercle.
Dans de nombreux cas, les approximations 3,14 ou 22/7 suffisent, bien que les ingénieurs aient longtemps utilisé 3,1416 (5 chiffres significatifs) ou 3,14159 (6 chiffres significatifs) pour plus de précision. Les approximations 22/7 et 355/113, avec respectivement 3 et 7 chiffres significatifs, sont obtenues à partir de l’écriture en fraction continue de π. Cependant c’est le mathématicien chinois Zu Chongzhi (祖沖之 en sinogrammes traditionnels, 祖冲之 en sinogrammes simplifiés, Zǔ Chōngzhī en piyin) (429–500) qui a découvert la fraction 355/113 en utilisant la méthode d’Archimède pour calculer le périmètre du polygone régulier à 12 288 côtés inscrit dans un cercle. Aujourd'hui, les approximations numériques le plus souvent utilisées par les ingénieurs sont celles de constantes informatiques prédéfinies.
L’approximation de π en 355/113 est la meilleure qui puisse être exprimée avec uniquement 3 chiffres au numérateur et au dénominateur. L’approximation 103 993 / 33 102 (qui fournit 10 chiffres significatifs) en exige un nombre beaucoup plus important : ceci venant de l’apparition du nombre élevé 292 dans le développement en fraction continue de π77.
Srinivasa Ramanujan propose également une approximation de π avec cette formule: , qui approche π avec tout de même 8 décimales78.
, qui approche π avec tout de même 8 décimales78.
Sur des microprocesseurs de la famille x86, les unités de calcul matérielles (FPU) sont capables de représenter des nombres flottants sur 80 bits (utilisables avec cette précision en langage C ou C++ avec le type
Pour les plateformes ou langages ne supportant nativement que les nombres en « simple précision », codés dans la norme IEEE 754 sur 32 bits utiles, pourront être pris en charge 7 chiffres significatifs (le minimum de précision supporté en langage C par le type

Cependant, il existe des fractions continues généralisées représentant π dont la structure est régulière : 81
81 82
82 83
83 84.
84.
Comme dit précédemment, on ignore encore si π est un nombre normal, ou même un nombre univers en base 10.
Une tradition anglo-saxonne veut que l’on fête l’anniversaire de π dans certains départements mathématiques des universités le 14 mars. Le 14 mars qui est noté « 3/14 » en notation anglo-saxonne, est donc appelé la journée de pi.
Il est en tout cas certain que π soit présent dans la culture artistique moderne. Par exemple, dans Contact, un roman de Carl Sagan, pi joue un rôle clé dans le scénario et il est suggéré qu’il y ait un message enfoui profondément dans les décimales de pi, placé par celui qui a créé l’univers. Cette partie de l’histoire a été écartée de l’adaptation cinématographique du roman.
Sur le plan cinématographique, Pi a servi de titre au premier long-métrage de Darren Aronofsky, à qui l’on doit notamment Requiem for a Dream. Pi est un thriller mathématique sur la découverte de la séquence parfaite, révélant ainsi formule exacte des marchés boursiers de Wall Street ou encore le véritable nom de Dieu.
Dans le registre musical, l’auteur-compositrice-interprète Kate Bush a sorti en 2005 son album Aerial, qui contenait le morceau « π », dont les paroles sont principalement composées des décimales de π91.
Au-delà de la mémorisation de Pi, usuellement ses 3 à 6 premiers chiffres ou par la remarquable valeur approchée de la fraction 355/113 (7 chiffres significatifs), la mémorisation d’un nombre record de décimales de π a longtemps été et demeure une obsession pour de nombreuses personnes. Le , à Oxford, le jeune autiste Asperger Daniel Tammet récite (en 5 heures, 9 minutes et 24 secondes) 22 514 décimales. En 2006, Akira Haraguchi, un ingénieur japonais retraité, a réussi à réciter 100 000 décimales de π en 16 heures92. Ceci, cependant, n’a pas encore été vérifié par le Livre Guinness des records. Le record de mémorisation de π reconnu par le Guinness des records est de 67 890 chiffres, détenu par Lu Chao, un jeune diplômé chinois93. Il lui a fallu 24 heures et 4 minutes pour réciter les 67 890 premières décimales de π sans erreur94.
Le 17 juin 2009, Andriy Slyusarchuk (en), un neurochirurgien et professeur ukrainien, a affirmé avoir mémorisé 30 millions de décimales de π, qui ont été imprimées en 20 volumes95. Bien qu’il n’ait pas récité les 30 millions de chiffres qu’il a dit avoir retenus (ce qui, au demeurant, lui aurait pris plus d'un an), certains médias prétendent qu’il était en mesure de réciter dix décimales sélectionnées aléatoirement parmi les volumes imprimés[réf. souhaitée]. La comparaison avec les valeurs officiellement retenues par le Guinness des records amène cependant les experts à mettre sérieusement en doute cette affirmation[réf. souhaitée].
Il y a plusieurs façons de retenir les décimales de π, dont des poèmes dont le nombre de lettres de chaque mot correspond à une décimale, les mots de dix lettres représentant un 0. En voici un exemple96 :
Cette méthode présente ses limites pour la mémorisation d’un très
grand nombre de décimales, où il semble plus opportun d’utiliser des
méthodes comme la méthode des loci99,100.
Sa valeur approchée par défaut à moins de 0,5×10–15 près2 est 3,141 592 653 589 793 en écriture décimale3,4.
De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques5.
Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine6.
La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
L’usage de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec —, n’est apparu qu’au XVIIIe siècle. Auparavant, sa valeur était désignée par diverses périphrases comme la « constante du cercle » ou son équivalent dans diverses langues.
Sommaire
Définition et premières propriétés
Définition
On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un disque égale son demi-périmètre multiplié par son rayon.
- π = P/(2r) = P/d.
- π = A/r2.
Il s’avère que cette définition géométrique, historiquement la première et très intuitive, n’est pas la plus directe pour les mathématiciens quand ils veulent définir π en toute rigueur. Les ouvrages plus spécialisés9 définissent π par l’analyse réelle à l’aide des fonctions trigonométriques elles-mêmes introduites sans référence à la géométrie (voir plus bas).
Autres définitions
- Un choix fréquent est de définir π comme le double du plus petit nombre positif x tel que cos(x) = 0, où cos est définie comme la partie réelle de l’exponentielle complexe10.
- Une autre définition est envisageable en considérant les propriétés
exp(z + w) = exp(z).exp(w) et exp(0) = 1 qui découlent de la définition
analytique de l’exponentielle et qui font que l’application t ↦ exp(it) est un morphisme de groupes continu du groupe (ℝ, +) vers le groupe
 (où
(où  est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme aℤ où a est un réel strictement positif. On pose alors π = a/211.
Le calcul intégral permet ensuite de vérifier que cette définition
abstraite correspond bien à celle de la géométrie euclidienne.
est l’ensemble des complexes de module égal à 1). On démontre alors que l’ensemble des nombres réels t tels que exp(it) = 1 est de la forme aℤ où a est un réel strictement positif. On pose alors π = a/211.
Le calcul intégral permet ensuite de vérifier que cette définition
abstraite correspond bien à celle de la géométrie euclidienne. - Le groupe Bourbaki propose une autre définition très voisine en démontrant l’existence d’un morphisme de groupe f continu de (ℝ, +) vers
 tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f' (x) = 2ia f(x). Il définit π comme le réel ainsi trouvé11.
tel que f(1/4) = i. Il démontre que ce morphisme est périodique de période 1, dérivable et qu’il existe un réel a tel que, pour tout réel x, f' (x) = 2ia f(x). Il définit π comme le réel ainsi trouvé11.
- Mais on peut aussi définir π grâce au calcul intégral en posant :

ce qui revient à calculer (par exemple comme limite de sommes de Riemann) l’aire d’un quart de disque de rayon 1. - Ou bien à l’aide du dénombrement, en appelant
 le nombre de couples d’entiers naturels (k, p) tels que k2 + p2 ≤ n2 et en définissant :
le nombre de couples d’entiers naturels (k, p) tels que k2 + p2 ≤ n2 et en définissant :

ce qui est une autre méthode pour calculer la surface du quart de disque.
Irrationalité
Le nombre π est irrationnel, ce qui signifie qu’on ne peut pas écrire π = p/q où p et q seraient des nombres entiers. Al-Khawarizmi, au IXe siècle, est persuadé que π est irrationnel12. Moïse Maïmonide fait également état de cette idée durant le XIIe siècle. Ce n’est cependant qu’au XVIIIe siècle que Johann Heinrich Lambert prouve ce résultat13.Ce dernier expose en 1761, dans son ouvrage Mémoires sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques, un développement en fraction continue généralisée de la fonction tangente. Il en déduit qu'un développement de tan(m/n), avec m et n des nombres entiers non nuls, s’écrit14 :

Avec la notation d'Alfred Pringsheim où :
Au cours du XXe siècle, d’autres démonstrations furent trouvées, celles-ci ne demandant pas de connaissances plus avancées que celle du calcul intégral. L’une d’entre elles, due à Ivan Niven, est très largement connue15,16. Une preuve similaire, version simplifiée de celle de Charles Hermite17,18, avait été trouvée quelque temps auparavant par Mary Cartwright19.
Transcendance
Le nombre π est même transcendant, c'est-à-dire non algébrique : il n'existe pas de polynôme à coefficients rationnels dont π soit une racine20.C'est au XIXe siècle que ce résultat est démontré. En 1873, Hermite prouve que la base du logarithme népérien, le nombre e, est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (le théorème d'Hermite-Lindemann) qui stipule que, si x est algébrique et différent de zéro, alors ex est transcendant. Or eiπ est algébrique (puisqu'il est égal à -1). Par contraposition, iπ est transcendant, donc comme i est algébrique, π est transcendant.
Une conséquence importante de la transcendance de π est que celui-ci n'est pas constructible. En effet, le théorème de Wantzel énonce en particulier que tout nombre constructible est algébrique. En raison du fait que les coordonnées de tous les points pouvant se construire à la règle et au compas sont des nombres constructibles, la quadrature du cercle est impossible ; autrement dit, il est impossible de construire, uniquement à la règle et au compas, un carré dont la superficie serait égale à celle d'un cercle donné21.
Représentation décimale
Les 16 premiers chiffres de l’écriture décimale de π sont 3,141 592 653 589 793 (voir les liens externes3,4,22 pour davantage de décimales).Alors qu’en 2007, on connaissait déjà plus de 1012 décimales de π23, de nombreuses applications concrètes, comme l’estimation de la circonférence d’un cercle, n’ont besoin que d’une dizaine de chiffres. Par exemple, la représentation décimale de π tronquée à 39 décimales est suffisante pour estimer la circonférence d’un cercle dont les dimensions sont celles de l’univers observable avec une précision comparable à celle du rayon d’un atome d’hydrogène24,25.
Étant donné que π est un nombre irrationnel, sa représentation décimale n’est pas périodique et ne prend pas fin. La séquence des décimales de π a toujours fasciné les mathématiciens professionnels et amateurs, et beaucoup d’efforts ont été mis en œuvre afin d’obtenir de plus en plus de décimales et d’en rechercher certaines propriétés26, comme l'occurrence de nombres premiers dans les concaténations de ses décimales (voir la section d'article Nombre premier issu de troncature de constante.)
Malgré les importants travaux d’analyse effectués et les calculs qui ont réussi à déterminer plus de 200 milliards de décimales de π, aucun modèle simple n’a été trouvé pour décrire la séquence de ces chiffres27. Les chiffres de la représentation décimale de π sont disponibles sur de nombreuses pages web, et il existe des logiciels de calcul des décimales de π qui peuvent en générer des milliards et qu’on peut installer sur un ordinateur personnel.
Par ailleurs, le développement décimal de π ouvre le champ à d’autres questions, notamment celle de savoir si π est un nombre normal, c’est-à-dire que ses chiffres en écriture décimale sont équirépartis. On peut aussi se demander si π est un nombre univers, ce qui signifie qu’on pourrait trouver dans son développement décimal n’importe quelle suite finie de chiffres. En 2006, il n’existait pas de réponse à ces questions28.
Représentation fractionnaire
Les fractions de nombres entiers suivantes sont utilisées pour mémoriser ou approcher pi dans des calculs (nombre de chiffres significatifs exacts entre parenthèses) :
Voir ci-dessous pour d’autres approches fractionnaires (Histoire, Approximation numérique, fractions continues et Mémorisation de π).
Approximation de π
On peut trouver une valeur approchée de π de façon empirique, en traçant un cercle, puis en mesurant son diamètre et sa circonférence, puis en divisant la circonférence par le diamètre. Une autre approche géométrique, attribuée à Archimède, consiste à calculer le périmètre Pn d’un polygone régulier à n côtés et à mesurer le diamètre d de son cercle circonscrit, ou celui de son cercle inscrit29. Plus le nombre de côtés du polygone est grand, meilleure est la précision obtenue pour la valeur de π.Archimède a utilisé cette approche en comparant les résultats obtenus par la formule en utilisant deux polygones réguliers ayant le même nombre de côtés, pour lesquels le cercle est pour l’un circonscrit et pour l’autre inscrit. Il a réussi, avec un polygone à 96 côtés, à déterminer30 que 3 + 10/71 < π < 3 + 1/7.
On peut également obtenir des valeurs approchées de π en mettant en œuvre des méthodes plus modernes. La plupart des formules utilisées pour calculer π se basent sur la trigonométrie et le calcul intégral. Cependant, certaines sont particulièrement simples, comme la formule de Leibniz31 :

Cette série converge si lentement que près de 200 termes sont nécessaires pour calculer π avec deux décimales exactes32. Cependant, il est possible de définir une suite similaire qui converge vers π beaucoup plus rapidement, en posant :
 et en définissant :
et en définissant : 
Le calcul de π10,10 demande alors un temps similaire à celui requis pour calculer les 150 premiers termes de la série initiale, mais la précision est bien meilleure car π10,10 = 3,141592653… approche π avec neuf décimales exactes33. On trouvera plus loin des méthodes de calcul plus élaborées, donnant des convergences bien plus rapides encore.
Histoire
L’histoire ancienne de π, qu’on peut retracer grâce aux écrits disponibles, suit approximativement l’avancée des mathématiques dans leur ensemble30. Certains auteurs divisent l’histoire de π en trois parties : la période antique durant laquelle π a été étudié géométriquement, l’ère classique, aux alentours du XVIIe siècle, où les outils du calcul intégral ont permis des avancées dans la connaissance du nombre π, et la période des ordinateurs numériques34.Antiquité
Il semble que, très tôt, les mathématiciens aient été convaincus qu'il existait un rapport constant entre le périmètre du cercle et son diamètre, ainsi qu'entre l'aire du disque et le carré du rayon. Des tablettes babyloniennes datant de 2 000 ans av. J.-C. et découvertes en 193635 présentent des calculs d'aire conduisant à une valeur de π de 3 + 1/836.
Ce recouvrement imparfait de l'aire du disque par un octogone peut
conduire à une approximation de l'aire du disque, et donc du nombre π.
Une justification possible de celle-ci s'appuie sur le schéma ci-contre. Si le disque a pour diamètre 9. L'aire du disque est légèrement supérieure à l'aire de l'octogone (irrégulier) obtenu en rognant les coins du carré de côté 9. Cet octogone a pour aire 63, l'aire du disque est alors évaluée à 64 soit l'aire d'un carré de côté 8. Le rapport entre l'aire du disque et le carré du rayon est alors évalué par 64/(9/2)2, c'est-à-dire 256/8137. Mais l'hypothèse que ce procédé ait conduit à l'approximation du papyrus Rhind ne fait pas l'unanimité chez les historiens.
Vers 700 av. J.-C., le texte indien Shatapatha Brahmana donne une approximation de π : 25/8 (= 3,125) et le Baudhāyana Sulbasūtra en donne deux autres : 900/289 (≈ 3,11) et 1156/361 (≈ 3,20)38. Des calculs d'astronomie ont ensuite conduit à une autre approximation védique : 339/108 (≈ 3,139)39. Au début du VIe siècle ap. J.-C., Aryabhata donne une approximation plus précise :
 = 3,1416. Comme |π – 3,1416| < 0,0000075, il s'agit d'un résultat remarquable, exact à 10−5 près.
= 3,1416. Comme |π – 3,1416| < 0,0000075, il s'agit d'un résultat remarquable, exact à 10−5 près.C'est dans le traité d'Archimède (287 à 212 av. J.-C.) intitulé De la mesure du cercle que l'on peut lire une démonstration liant l'aire du disque et l'aire du triangle ayant une base de longueur le périmètre du cercle et pour hauteur le rayon, démontrant ainsi qu'une même constante apparaît dans le rapport entre aire du disque et carré du rayon et entre périmètre et diamètre40.
Cette démonstration s'appuie sur la méthode d'exhaustion et un raisonnement par l'absurde41. En partant d'un carré inscrit dans le cercle et d'un carré circonscrit au cercle et en multipliant indéfiniment par 2 le nombre de côtés, il prouve que l'aire du disque ne peut être inférieure ni supérieure à celle du triangle correspondant.
Déroulement des 8 portions.
Encadrement de Liu Hui.
Formules et calculs jusqu’en 1900
Jusqu’en 1400 environ, la précision des approximations de π n’excédait pas les 10 décimales. Les progrès en matière de calcul intégral et de séries vont permettre d’améliorer cette précision. Les séries permettent d’approcher π avec d’autant plus de précision qu’on utilise de termes de la série pour le calcul. Vers 1400, Madhava de Sangamagrama trouve ce qui constitue, en langage moderne, le développement de la fonction arc tangente (redécouvert par James Gregory et Gottfried Wilhelm Leibniz au XVIIe siècle) :
![\arctan(x)=x-\frac{x^3}3+\frac{x^5}5-\frac{x^7}7+\cdots=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{2k+1}\quad (x \in \left[-1,1\right]).](https://upload.wikimedia.org/math/7/8/4/784c0a7223978b13c2c8e2cbb361c057.png) Le cas particulier x = 1 est la série de Leibniz mentionnée plus haut — également connue sous le nom de série de Madhava-Leibniz47,48 — dont la convergence est trop lente.
Le cas particulier x = 1 est la série de Leibniz mentionnée plus haut — également connue sous le nom de série de Madhava-Leibniz47,48 — dont la convergence est trop lente.Le cas particulier x = 1/√3 :
 converge bien plus vite, ce qui a permis à Madhava de donner une valeur approchée de π de 3,141 592 653 59, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi (Traité de la circonférence), qui a réussi à donner 16 décimales.
converge bien plus vite, ce qui a permis à Madhava de donner une valeur approchée de π de 3,141 592 653 59, qui a 11 décimales correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kachi (Traité de la circonférence), qui a réussi à donner 16 décimales.La première contribution importante venant d’Europe depuis Archimède a été faite par François Viète, qui en donne douze décimales, avec un encadrement du reste dans son Canon mathématique en 1579. Il est suivi par Adrien Romain, qui donne 15 décimales en 1591, et l’Allemand Ludolph van Ceulen (1540–1610), qui a utilisé la même méthode géométrique afin de donner une estimation de π correcte à 35 décimales près. Il a été si fier de son calcul, qui lui a demandé une grande partie de sa vie, qu’il a fait graver les décimales sur sa pierre tombale49.
Il est immédiatement suivi par Willebrord Snell, son élève, qui trouve des méthodes plus rapides pour obtenir la même approximation. Dans la même période, les méthodes de calcul intégral et de détermination de séries et produits infinis pour des quantités géométriques ont commencé à émerger en Europe. La première formule de ce type est la formule de Viète (en) :
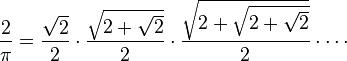
exposée par François Viète en 1579 dans son Canon mathématique et à nouveau[réf. souhaitée] en 1593, dans ses Problèmes variés. Un autre résultat célèbre est le produit de Wallis :

que l’on doit à John Wallis, qui l’a mis en évidence en 1655. Isaac Newton lui-même a utilisé le développement en série de π/6 = arcsin(1/2)50 pour calculer 15 décimales de π ; bien plus tard, il a déclaré : « J’ai honte de vous dire combien de décimales j’ai trouvées grâce à ces calculs, n’ayant aucune autre occupation à l’époque. »51.
En 1706, John Machin a été le premier à trouver 100 décimales de π, en utilisant la formule :
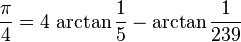 et le développement ci-dessus en série entière de arctan.
et le développement ci-dessus en série entière de arctan.Les formules de ce type, maintenant connues sous le nom de formules de Machin, ont été utilisées pour battre plusieurs records de décimales connues de π, et demeurent aujourd’hui les formules les plus connues pour calculer π grâce à des ordinateurs. Un record remarquable est détenu par le calculateur prodige Johann Dase qui, en 1844, à l’aide d’une formule de Machin, a calculé de tête 200 décimales de π, à la demande de Gauss. La meilleure valeur obtenue à la fin du XIXe siècle est due à William Shanks, qui a passé quinze ans à calculer 707 décimales de π, bien qu’à cause d’une erreur, seules les 527 premières étaient correctes. De nos jours, il est aisé d’éviter de telles erreurs, en faisant faire les calculs par l’ordinateur, et en utilisant deux formules différentes pour éliminer les risques d’erreur de calcul, de programmation, ou du microprocesseur.
Les avancées théoriques du XVIIIe siècle ont amené les mathématiciens à s’interroger sur la nature de π, notamment sur l’absence de motifs périodiques dans ses décimales, une hypothèse raisonnable au vu des calculs numériques, mais pour laquelle il fallait une approche radicalement différente pour la prouver rigoureusement. Ce tour de force a été réalisé par Johann Heinrich Lambert en 1761, qui fut ainsi le premier à prouver l’irrationalité de π, par la suite Adrien-Marie Legendre a aussi prouvé que π2 aussi était irrationnel. Cette constante (π2) jouait un rôle notable en mathématique, puisqu’elle apparaissait dans la solution du problème de Bâle, qui consistait à trouver la valeur exacte de
 qui est π2/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.
qui est π2/6 (comme prouvé par Leonhard Euler qui a établi à cette occasion une connexion profonde entre π et les nombres premiers). Dans la foulée, Legendre et Euler ont tous les deux conjecturé que π était un nombre transcendant, ce qui a finalement été prouvé en 1882 par Ferdinand von Lindemann.Origine de la notation
C’est au cours du XVIIIe siècle que s’établit l’usage de la lettre grecque « π », première lettre du mot grec περιφέρεια (périphérie, c’est-à-dire circonférence), pour le rapport de la circonférence du cercle sur son diamètre52.À partir du XVIIe siècle certains mathématiciens utilisent la notation π/δ où π désigne la circonférence et δ le diamètre53. Le premier à utiliser simplement π est William Jones52 dans son livre Synopsis palmariorum mathesios publié en 1706, à propos du calcul astucieux de ce nombre par la série de son ami Machin. Les mathématiciens continuent cependant d’utiliser d’autres notations. Parmi ceux-ci Euler se met à la notation de Jones54 dans sa correspondance à partir de 1736. Il l’adopte dans son livre Introductio in analysin infinitorum publié en 1748, ce qui eut certainement une grande influence. La notation finit par s’imposer vers la fin du XVIIIe siècle55.
Ère informatique
Alors que quelques dizaines de décimales de π sont largement suffisantes pour les calculs pratiques qu’effectue un physicien, la conquête des décimales du nombre π n’a pas cessé avec l’arrivée des ordinateurs, qui ont permis de calculer un très grand nombre de ces décimales.En 1949, à l’aide de l’ENIAC, John von Neumann a obtenu 2037 décimales de π, à la suite d'un calcul qui a duré 70 heures56,57. Des milliers de décimales supplémentaires ont été trouvées au cours des décennies suivantes, l’étape du million de chiffres ayant été passée en 1973. Les progrès n’ont pas seulement été dus aux ordinateurs de plus en plus rapides, mais aussi aux nouveaux algorithmes utilisés. L’une des avancées les plus significatives a été la découverte de la transformée de Fourier rapide dans les années 1960, qui a permis aux ordinateurs de manipuler rapidement de très grands nombres.
Au début du XXe siècle, le mathématicien indien Srinivasa Ramanujan a trouvé de nombreuses nouvelles formules faisant intervenir π ; certaines d’entre elles sont remarquables par leur élégance et leur profondeur mathématique58. L’une de ces formules est la série suivante :

La formule ci-dessous, possédant un lien étroit avec celle énoncée ci-dessus, a été découverte par David et Gregory Chudnovsky en 1987 :

Cette formule donne 14 nouvelles décimales de π à chaque terme58. Vers la fin des années 1980, les frères Chudnovsky l’ont utilisée pour battre plusieurs records de décimales de π calculées. Elle demeure la formule la plus utilisée pour calculer π sur des ordinateurs personnels.
Lemniscate de Bernoulli.
 où r représente la distance OA entre le centre et un sommet de la lemniscate et où
où r représente la distance OA entre le centre et un sommet de la lemniscate et où 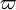 est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1, √2) alors :
est la constante de la lemniscate. Si on note G, la constante de Gauss, c’est-à-dire l’inverse de M(1, √2) alors :  Salamin et Brent ont utilisé ce résultat pour construire l’algorithme
qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √260.
Salamin et Brent ont utilisé ce résultat pour construire l’algorithme
qui porte leur nom, et grâce auquel la conquête des décimales de π va alors avancer conjointement avec celle des décimales de √260.L’algorithme consiste à poser :
 , puis à définir les relations de récurrence suivantes :
, puis à définir les relations de récurrence suivantes : 
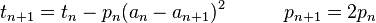 et enfin à calculer ces termes jusqu’à ce que an et bn soient assez proches. On a alors une valeur approchée de π donnée par :
et enfin à calculer ces termes jusqu’à ce que an et bn soient assez proches. On a alors une valeur approchée de π donnée par : 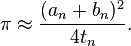
En utilisant cet algorithme, seuls 25 termes sont nécessaires pour calculer 45 millions de décimales. Un algorithme similaire qui quadruple la précision à chaque étape a été trouvé par Jonathan et Peter Borwein61. C’est grâce à ces méthodes qu’en 1999, Yasumasa Kanada et son équipe ont battu le record du nombre de décimales de π qui datait de 1980, en atteignant les 206 158 430 000 chiffres.
En 1997, la formule BBP, découverte par Simon Plouffe, a fait de nouveau progresser la connaissance de π62. La formule,
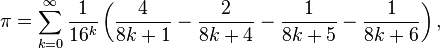 est remarquable car elle permet de calculer n’importe quel chiffre de l’écriture de π en base hexadécimale ou binaire, sans calculer les précédents62. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000e chiffre en binaire de π, qui s’est révélé être 063.
est remarquable car elle permet de calculer n’importe quel chiffre de l’écriture de π en base hexadécimale ou binaire, sans calculer les précédents62. Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé une variante de la formule BBP due à Fabrice Bellard pour calculer le 1 000 000 000 000 000e chiffre en binaire de π, qui s’est révélé être 063.Si une formule de la forme :
 était trouvée, avec b et c des entiers positifs et p et q
des polynômes de degrés fixés à coefficients entiers (comme pour la
formule BBP ci-dessus), ce serait l’un des moyens les plus efficaces
pour calculer n’importe quel chiffre dans l’écriture de π en base bc sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé[pas clair] et du degré des polynômes.
était trouvée, avec b et c des entiers positifs et p et q
des polynômes de degrés fixés à coefficients entiers (comme pour la
formule BBP ci-dessus), ce serait l’un des moyens les plus efficaces
pour calculer n’importe quel chiffre dans l’écriture de π en base bc sans avoir à calculer les précédents, en un temps dépendant uniquement du nombre de termes de la série calculé[pas clair] et du degré des polynômes.En 2006, Simon Plouffe a trouvé plusieurs formules faisant intervenir π64. En posant q = eπ (constante de Gelfond), on a :

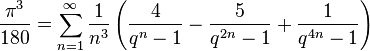 ainsi que :
ainsi que :  où k est un nombre impair, et a, b, c sont des nombres rationnels.
où k est un nombre impair, et a, b, c sont des nombres rationnels.En août 2010, le record est à nouveau battu par deux informaticiens (un japonais et un américain) avec 5 000 milliards de décimales65.
Le 8 octobre 2014, le nouveau record est 13 300 milliards de décimales66.
Utilisation en mathématiques et en sciences
Géométrie
π apparaît dans de nombreuses formules de géométrie impliquant les cercles et les sphères :| Forme géométrique | Formule |
|---|---|
| Circonférence d’un cercle de rayon r et de diamètre d |  |
| Aire d’un disque de rayon r |  |
| Aire d’une ellipse de demi-axes a et b | 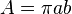 |
| Volume d’une boule de rayon r |  |
| Aire surfacique d’une sphère de rayon r |  |
| Volume d’un cylindre de hauteur h et de rayon r | 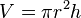 |
| Aire surfacique d’un cylindre de hauteur h et de rayon r |  |
| Volume d’un cône de hauteur h et de rayon r | 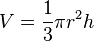 |
| Aire surfacique d’un cône de hauteur h et de rayon r |  |
Nombres complexes
La formule d’Euler illustrée dans le plan complexe. Une augmentation de l’angle φ de π radians (180°) donne l’identité d’Euler.

L’apparition fréquente de π en analyse complexe a pour origine le comportement de la fonction exponentielle complexe, décrite par la formule d’Euler :
 où i est l’unité imaginaire satisfaisant la relation i2 = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360° = 2π rad. En particulier, une rotation de 180° = π rad donne l’identité d'Euler
où i est l’unité imaginaire satisfaisant la relation i2 = −1 et e ≈ 2.71828 est la constante de Néper. Cette formule implique que les puissances imaginaires de e décrivent des rotations sur le cercle unité du plan complexe ; ces rotations ont une période de 360° = 2π rad. En particulier, une rotation de 180° = π rad donne l’identité d'Euler 
Cette formule a été qualifiée de « formule la plus remarquable des mathématiques » par Richard Feynman, car elle réunit en seulement 7 caractères l’addition, la multiplication, l’exponentiation, l’égalité et les constantes remarquables 0, 1, e, i et π67.
Suites et séries
De nombreuses suites ou séries convergent vers π ou un multiple rationnel de π et sont même à l’origine de calculs de valeurs approchées de ce nombre.Méthode d’Archimède

Les deux suites définies par sn = n sin(π/n) et tn = n tan(π/n), n ≥ 3, représentent les demi-périmètres des polygones réguliers à n côtés, inscrit dans le cercle trigonométrique pour sn, exinscrit pour tn. On les exploite par des suites extraites dont l’indice (le nombre de côtés du polygone) double à chaque itération, pour obtenir π par passage à la limite d’expressions utilisant les opérations arithmétiques élémentaires et la racine carrée. Ainsi, on peut s’inspirer de la méthode utilisée par Archimède — voir historique du calcul de π — pour donner une définition par récurrence des suites extraites de termes s2n et t2n ou encore s3.2n et t3.2n, à l’aide des identités trigonométriques usuelles :
 (voir pour t2n identité trigonométrique#Formules d'angle moitié -- seconde formule, et pour s2n, 2sin2 α/2 = sin α tan α/2 qui se déduit de identité trigonométrique#Formules d'angle double -- première formule).
(voir pour t2n identité trigonométrique#Formules d'angle moitié -- seconde formule, et pour s2n, 2sin2 α/2 = sin α tan α/2 qui se déduit de identité trigonométrique#Formules d'angle double -- première formule).En utilisant directement les identités trigonométriques 2sin(x/2) = √2 – 2cos(x) et 2cos(x/2) = √2 + 2cos(x) (x ∈ [0, π]), on peut exprimer s2k+1 et s3×2k (pour k ≥ 1), puis π (par passage à la limite) sous forme de formules où s’emboîtent des racines carrées :
 (k est le nombre de racines carrées) ou encore :
(k est le nombre de racines carrées) ou encore :  Les deux formules trigonométriques se démontrent simplement géométriquement par le théorème de Pythagore, aussi le même raisonnement peut-il se faire directement sur les suites sn et tn vues comme demi-périmètres de polygones réguliers, sans référence à la trigonométrie.
Les deux formules trigonométriques se démontrent simplement géométriquement par le théorème de Pythagore, aussi le même raisonnement peut-il se faire directement sur les suites sn et tn vues comme demi-périmètres de polygones réguliers, sans référence à la trigonométrie.Une autre expression de s2k+1, qui peut se déduire simplement de la première de ces deux égalités (multiplier par √2+√…), conduit au produit infini suivant (formule de François Viète, 1593) :

Sommes et produits infinis
 (formule de Leibniz, James Gregory et Madhava de Sangamagrama68,69)
(formule de Leibniz, James Gregory et Madhava de Sangamagrama68,69) (produit de Wallis)
(produit de Wallis)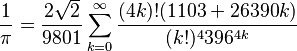 (formule due à Ramanujan)
(formule due à Ramanujan)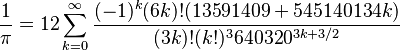 (formule due à David et Gregory Chudnovsky)
(formule due à David et Gregory Chudnovsky)
Suites récursives
Suite inspirée de la formule de Brent-Salamin (1975) :Soient trois suites
 ,
,  et
et  se définissant mutuellement :
se définissant mutuellement :  ; on a :
; on a : 
Le nombre de décimales correctes (en base 10) double presque à chaque itération.
Fonction zêta de Riemann
Articles détaillés : Problème de Bâle et Fonction zêta de Riemann.
 (Euler)
(Euler) ,
,
Suite logistique
Soit (xn) la suite des itérés de la fonction logistique de paramètre μ = 4 appliquée à un réel x0 choisi dans l’intervalle [0, 1] (c’est-à-dire qu’on définit, pour tout n ≥ 0, ). La suite (xn) quitte l’intervalle [0, 1] et diverge pour quasiment toutes les valeurs initiales.
). La suite (xn) quitte l’intervalle [0, 1] et diverge pour quasiment toutes les valeurs initiales.On a
 pour presque toutes les valeurs initiales x0.
pour presque toutes les valeurs initiales x0.Intégrale
Le nombre π apparait également comme étant le double de la limite du sinus intégral à l’infini : 2
Probabilités et statistiques
En probabilités et en statistiques, il existe de nombreuses lois qui utilisent la constante π, dont :- la loi normale d’espérance μ et d’écart type σ, dont la densité de probabilité s’écrit70 :

- la loi de Cauchy, dont la densité de probabilité est71 :

D’autre part, il existe diverses expériences probabilistes où π intervient dans la probabilité théorique. Elles peuvent donc servir, en effectuant un grand nombre d’épreuves, à déterminer une approximation de π.
L’aiguille de Buffon est une expérience de probabilité proposée par Georges-Louis Leclerc, comte de Buffon et consistant à calculer la probabilité qu’une aiguille de longueur a, lancée sur une parquet fait de lattes de largeur L, soit à cheval sur deux lattes, cette probabilité p est72 :
 même si l'aiguille est courbe73,74.
même si l'aiguille est courbe73,74.Cette formule peut être utilisée pour déterminer une valeur approchée de π :
 où n est le nombre d’aiguilles lancées, et x celui d’aiguilles qui sont sur deux lattes à la fois.
où n est le nombre d’aiguilles lancées, et x celui d’aiguilles qui sont sur deux lattes à la fois.Cette méthode présente rapidement ses limites ; bien que le résultat soit mathématiquement correct, il ne peut pas être utilisé pour déterminer plus que quelques décimales de π expérimentalement. Pour obtenir seulement une valeur approchée de 3,14, il est nécessaire d’effectuer des millions de lancers72, et le nombre de lancers nécessaires croît exponentiellement avec le nombre de décimales voulu. De plus, une très faible erreur dans la mesure des longueurs L et a va se répercuter de façon importante sur la valeur trouvée de π. Par exemple, une différence de mesure d’un seul atome sur une aiguille de longueur de 10 centimètres va se retrouver dès la neuvième décimale de π. En pratique, les cas où l’aiguille semble toucher exactement la limite entre deux lattes va accroître l’imprécision de l’expérience, de sorte que les erreurs apparaîtront bien avant la neuvième décimale.
Évaluation de π par la méthode de Monte Carlo.
Propriétés avancées
Approximations numériques
Comme π est transcendant, il n’existe pas d’expression de ce nombre qui fasse uniquement appel à des nombres et des fonctions algébriques20. Les formules de calcul de π utilisant l’arithmétique élémentaire impliquent généralement les sommes infinies. Ces formules permettent d’approcher π avec une erreur aussi petite que ce que l’on désire76, sachant que plus on rajoute de termes dans le calcul, plus le résultat sera proche de π.Par conséquent, les calculs numériques doivent utiliser des approximations de π.
La première approximation numérique de π fut certainement 342. Dans les cas où une situation ne demande que peu de précision, cette valeur peut servir d’approximation convenable. Si 3 est une estimation par défaut, c’est parce qu’il est le rapport entre le périmètre d’un hexagone régulier inscrit dans un cercle et le diamètre de ce cercle.
Dans de nombreux cas, les approximations 3,14 ou 22/7 suffisent, bien que les ingénieurs aient longtemps utilisé 3,1416 (5 chiffres significatifs) ou 3,14159 (6 chiffres significatifs) pour plus de précision. Les approximations 22/7 et 355/113, avec respectivement 3 et 7 chiffres significatifs, sont obtenues à partir de l’écriture en fraction continue de π. Cependant c’est le mathématicien chinois Zu Chongzhi (祖沖之 en sinogrammes traditionnels, 祖冲之 en sinogrammes simplifiés, Zǔ Chōngzhī en piyin) (429–500) qui a découvert la fraction 355/113 en utilisant la méthode d’Archimède pour calculer le périmètre du polygone régulier à 12 288 côtés inscrit dans un cercle. Aujourd'hui, les approximations numériques le plus souvent utilisées par les ingénieurs sont celles de constantes informatiques prédéfinies.
L’approximation de π en 355/113 est la meilleure qui puisse être exprimée avec uniquement 3 chiffres au numérateur et au dénominateur. L’approximation 103 993 / 33 102 (qui fournit 10 chiffres significatifs) en exige un nombre beaucoup plus important : ceci venant de l’apparition du nombre élevé 292 dans le développement en fraction continue de π77.
Srinivasa Ramanujan propose également une approximation de π avec cette formule:
 , qui approche π avec tout de même 8 décimales78.
, qui approche π avec tout de même 8 décimales78.Constantes approchées prédéfinies en informatique
Dans les calculs numériques usuels sur ordinateur, on utilise plutôt une constante correctement arrondie mais prédéfinie avec une précision d’au moins 16 chiffres significatifs (c’est la meilleure précision représentable par un nombre en virgule flottante au format standard IEEE 754 sur 64 bits, un type généralement désigné « double précision ») et choisie afin que le calcul de son sinus retourne 0 exactement par une fonction définie dans cette même précision. Ainsi le fichier d’entête standard<math.h> utilisé en langage C ou C++ définit la constante M_PI
en double précision (le type flottant utilisé par défaut dans de
nombreuses fonctions des bibliothèques mathématiques standards) à la
valeur de 3,141 592 653 589 793 (parfois avec des chiffres
supplémentaires si la plateforme supporte une précision plus étendue
pour le type long double). La même valeur est utilisée en langage Java, qui s’appuie sur la même norme IEEE 754, avec la constante standard java.lang.Math.PI79).
On retrouve cette constante définie ainsi dans de nombreux langages de
programmation, avec la meilleure précision possible dans les formats de
nombres en virgule flottante supportés, puisque le type « double
précision » de la norme IEEE 754 s'est imposé comme une référence de
précision minimale nécessaire dans de nombreux langages pour
d’innombrables applications.Sur des microprocesseurs de la famille x86, les unités de calcul matérielles (FPU) sont capables de représenter des nombres flottants sur 80 bits (utilisables avec cette précision en langage C ou C++ avec le type
long double mais sans garantie de support matériel), ce qui porte la précision de π
à 19 chiffres significatifs. La dernière révision publiée en 2008 de la
norme IEEE 754 comporte aussi la définition de nombres en virgule
flottante en « quadruple précision » (ou quad) codés sur 128 bits, ce qui permettrait de définir une approximation de la constante π
avec une précision de 34 chiffres significatifs (toutefois cette
précision n’est pas encore prise en charge nativement par de nombreux
langages de programmation car peu de processeurs permettent cette
précision directement au niveau matériel sans un support logiciel
supplémentaire).Pour les plateformes ou langages ne supportant nativement que les nombres en « simple précision », codés dans la norme IEEE 754 sur 32 bits utiles, pourront être pris en charge 7 chiffres significatifs (le minimum de précision supporté en langage C par le type
float),
c’est-à-dire la constante correctement arrondie à 3,141593 et
équivalente en précision à celle donnée par la fraction 355/113 (cette
fraction permet aussi des calculs rapides dans des logiciels pour des
systèmes légers ne comportant pas d’unité matérielle de calcul en
virgule flottante).Fractions continues
La suite des dénominateurs partiels du développement en fraction continue de π ne fait apparaître aucun schéma évident80 :
Cependant, il existe des fractions continues généralisées représentant π dont la structure est régulière :
 81
81 82
82 83
83 84.
84.Questions ouvertes
De nombreuses questions se posent encore : π et e sont deux nombres transcendants mais sont-ils algébriquement indépendants ou bien existe-t-il une équation polynomiale à deux variables et à coefficients entiers dont le couple (π, e) soit une solution ? La question est encore en suspens. En 1929, Alexandre Gelfond prouve que eπ est transcendant60 et en 1996, Yuri Nesterenko (en) prouve que π et eπ sont algébriquement indépendants.Comme dit précédemment, on ignore encore si π est un nombre normal, ou même un nombre univers en base 10.
Culture populaire
Sans doute en raison de la simplicité de sa définition, le nombre pi et particulièrement son écriture décimale sont ancrés dans la culture populaire à un degré plus élevé que tout autre objet mathématique85. D’ailleurs, la découverte d’un plus grand nombre de décimales de π fait souvent l’objet d’articles dans la presse généraliste, signe que π est un objet familier même à ceux qui ne pratiquent pas les mathématiques86,87,88.Une tradition anglo-saxonne veut que l’on fête l’anniversaire de π dans certains départements mathématiques des universités le 14 mars. Le 14 mars qui est noté « 3/14 » en notation anglo-saxonne, est donc appelé la journée de pi.
π dans l’art
Nombreux sont les sites ou ouvrages qui signalent la présence du nombre π dans les pyramides et, plus précisément, que π est le rapport entre le périmètre de la base et le double de la hauteur des pyramides89. Il est vrai que la pyramide de Khéops possède une pente de 14/11, et que par conséquent, le rapport entre la base et la hauteur est de 22/14. Le rapport 22/7 étant une bonne approximation de π, le rapport entre le périmètre et le double de la hauteur de la pyramide de Khéops est bien voisin de π. Faut-il pour autant y chercher une intention ? Rien n’est moins sûr90 puisque la pente des pyramides n’est pas constante et que, selon les régions et les époques, on trouve des pentes de 6/5 (pyramide rouge), 4/3 (pyramide de Khephren) ou 7/5 (pyramide rhomboïdale) qui conduisent à un rapport entre périmètre et double de la hauteur éloigné de π.Il est en tout cas certain que π soit présent dans la culture artistique moderne. Par exemple, dans Contact, un roman de Carl Sagan, pi joue un rôle clé dans le scénario et il est suggéré qu’il y ait un message enfoui profondément dans les décimales de pi, placé par celui qui a créé l’univers. Cette partie de l’histoire a été écartée de l’adaptation cinématographique du roman.
Sur le plan cinématographique, Pi a servi de titre au premier long-métrage de Darren Aronofsky, à qui l’on doit notamment Requiem for a Dream. Pi est un thriller mathématique sur la découverte de la séquence parfaite, révélant ainsi formule exacte des marchés boursiers de Wall Street ou encore le véritable nom de Dieu.
Dans le registre musical, l’auteur-compositrice-interprète Kate Bush a sorti en 2005 son album Aerial, qui contenait le morceau « π », dont les paroles sont principalement composées des décimales de π91.
Mémorisation de π
Les récentes décennies ont vu une forte augmentation du record du nombre de décimales de π mémorisées.
Le 17 juin 2009, Andriy Slyusarchuk (en), un neurochirurgien et professeur ukrainien, a affirmé avoir mémorisé 30 millions de décimales de π, qui ont été imprimées en 20 volumes95. Bien qu’il n’ait pas récité les 30 millions de chiffres qu’il a dit avoir retenus (ce qui, au demeurant, lui aurait pris plus d'un an), certains médias prétendent qu’il était en mesure de réciter dix décimales sélectionnées aléatoirement parmi les volumes imprimés[réf. souhaitée]. La comparaison avec les valeurs officiellement retenues par le Guinness des records amène cependant les experts à mettre sérieusement en doute cette affirmation[réf. souhaitée].
Il y a plusieurs façons de retenir les décimales de π, dont des poèmes dont le nombre de lettres de chaque mot correspond à une décimale, les mots de dix lettres représentant un 0. En voici un exemple96 :
Que j’aime à faire apprendre un nombre utile aux sages !
Immortel Archimède, artiste, ingénieur, (variante : Glorieux Archimède, artiste ingénieux,)
Qui de ton jugement peut priser la valeur ? (variante : Toi de qui Syracuse aime encore la gloire,)
Pour moi ton problème eut de pareils avantages. (variante : Soit ton nom conservé par de savants grimoires.)97
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l’orbe calculée98 approchera ;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
Immortel Archimède, artiste, ingénieur, (variante : Glorieux Archimède, artiste ingénieux,)
Qui de ton jugement peut priser la valeur ? (variante : Toi de qui Syracuse aime encore la gloire,)
Pour moi ton problème eut de pareils avantages. (variante : Soit ton nom conservé par de savants grimoires.)97
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l’orbe calculée98 approchera ;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
Annexes
Bibliographie
- Numéro spécial π, Supplément au Petit Archimède, no 64-65, mai 1980
- Jean-Paul Delahaye, Le fascinant nombre π [détail de l’édition].
- Pierre Eymard et Jean-Pierre Lafon, Autour du nombre Pi, Éditions Hermann, Paris, 1999 (ISBN 2-7056-1443-5)
- Jörg Arndt et Christoph Haenel, À la poursuite de π, Éditions Vuibert, 2006 (ISBN 2-7117-7170-9)
- Reinhold Remmert, « Le nombre π », dans H.-D. Ebbinghaus (de) et al., Numbers, traduction française et adaptation de François Guénard, Les nombres. Leur histoire, leur place et leur rôle de l’Antiquité aux recherches actuelles, Vuibert, (ISBN 2-7117-8901-2)
- "Eliette Abécassis", "Le palimpseste d’Archimède" (Roman), Albin Michel, ISBN 978-2-226-24829-9
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pi » (voir la liste des auteurs).- On l'appelle parfois la constante d’Archimède, en raison de la contribution d'Archimède au calcul de l'aire d'un disque ou d'une sphère, et au fait qu'il ait été le premier à donner une méthode d'encadrement de Pi.
- Valeur
décimale exprimée sur 16 chiffres significatifs, soit la précision
maximale (pour pi) d’un nombre flottant en double précision au format
binaire sur 64 bits standard de l'IEEE, qui permet de stocker entre 15
et 17 chiffres décimaux significatifs (selon principalement la valeur du
premier chiffre décimal et éventuellement les suivants) ; ce format
binaire est utilisé dans de nombreux langages de programmation, par
exemple dans le type
doubledes langages C, C++, Java, etc; il est aujourd’hui pris en charge nativement par la plupart des microprocesseurs modernes et des bibliothèques mathématiques. - 128 000 premières décimales de π [archive].
- (en) Site permettant une recherche de chiffres dans les 200 000 000 premières décimales [archive].
- (en) Howard Whitley Eves, An Introduction to the History of Mathematics, Holt, Rinehart & Winston, (lire en ligne [archive]).
- La preuve de ce résultat en 1882 est due à Ferdinand von Lindemann.
- Par exemple le Petit Robert ou le TLFi ; voir « Pi (sens B) » [archive], Centre national de ressources textuelles et lexicales.
- (en) Bettina Richmond, « Area of a Circle » [archive], Western Kentucky University, .
- Par exemple J. Lelong-Ferrand, J.M. Arnaudiès, cours de mathématiques Tome 2, Dunod Université, 4e édition 1977.
- (en) Walter Rudin, Principles of Mathematical Analysis, McGraw-Hill, (ISBN 0-07-054235-X), p. 183.
- « Histoire du nombre pi » [archive], sur Math93.
- (en) Mustafa Mawaldi, Glimpses in the history of a great number: Pi in Arabic mathematics [archive].
- Johann Heinrich Lambert, « Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques », Histoire de l'Académie royale des sciences et des belles-lettres de Berlin, vol. XVII, , p. 265-322 (lire en ligne [archive]).
- Pour plus de détails voir Fraction continue et approximation diophantienne#Nombres à tangente rationnelle, dont π.
- (en) Ivan Niven, « A simple proof that π is irrational », Bulletin of the American Mathematical Society, vol. 53, no 6, , p. 509 (lire en ligne [archive]).
- (en) Helmut Richter, « Pi Is Irrational » [archive], Leibniz Rechenzentrum, .
- Charles Hermite, « Extrait d'une lettre de Monsieur Ch. Hermite à Monsieur Paul Gordan », Journal für die reine und angewandte Mathematik, vol. 76, , p. 303–311 (lire en ligne [archive]).
- Charles Hermite, « Extrait d'une lettre de Mr. Ch. Hermite à Mr. Borchardt », Journal für die reine und angewandte Mathematik, vol. 76, , p. 342–344 (lire en ligne [archive]).
- (en) Harold Jeffreys, Scientific Inference, Cambridge University Press, , 3e éd. (ISBN 978-0-52118078-8), 268 [archive].
- (en) Steve Mayer, « The Transcendence of π » [archive].
- (en) « Squaring the Circle » [archive], Cut The Knot.
- (en)oeis.org [archive] OEIS : suite A000796 donnant 20 000 décimales de Pi et liens vers d'autres sites.
- (en) « Current publicized world record of pi » [archive].
- (en) Robert M. Young, Excursions in Calculus, Washington, MAA (ISBN 0883853175, lire en ligne [archive]), p. 417.
- (en) « Statistical estimation of pi using random vectors » [archive].
- (en) Eric W. Weisstein, « Pi Digits [archive] », MathWorld.
- (en) Chad Boutin, « Pi seems a good random number generator - but not always the best » [archive], Purdue University, .
- Conférence de Jean-Paul Delahaye, Le nombre pi est-il simple ou compliqué ?, mardi 3 octobre 2006, Cité des sciences.
- (en) Rick Groleau, « Infinite Secrets: Approximating Pi » [archive], NOVA, .
- (en) Petr Beckmann, A History of Pi (en), Dorset Press, (1re éd. 1971, St. Martin's Griffin) (ISBN 978-0-88029418-8).
- (en) Pierre Eymard et Jean-Pierre Lafon, The Number π, AMS, (ISBN 0821832468, lire en ligne [archive]), p. 53.
- (en) Vito Lampret, « Even from Gregory-Leibniz series π could be computed: an example of how convergence of series can be accelerated », Lecturas Matemáticas, vol. 27, no 1, , p. 21-25 (lire en ligne [archive]).
- Pour plus d’information sur des méthodes analogues, voir Formule d’Euler-Maclaurin.
- (en) « Archimedes’ constant π » [archive].
- Tablettes de Suse — voir par exemple ici [archive].
- (en) Otto Neugebauer, The Exact Sciences in Antiquity, p. 47.
- (en) Victor J. Katz, History of Mathematics: An Introduction, Addison-Wesley, , 2e éd. (ISBN 0321016181), p. 20.
- (en) Subhash C. Kak, « Three old Indian values of π », Indian J. Hist. Sci., vol. 32, , p. 307-314 (lire en ligne [archive]).
- (en) Ian Pearce, « Mathematics in the service of religion: I. Vedas and Vedangas », dans MacTutor History of Mathematics archive, université de St Andrews, (lire en ligne [archive]).
- Voir une traduction du texte original [archive].
- Calcul infinitésimal - l'œuvre d'Archimède [archive], Encyclopædia Universalis
- (en) John J. O'Connor et Edmund F. Robertson, « A history of Pi », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne [archive])..
- (en) C. Boyer, A History of Mathematics, Wiley, p. 168.
- Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition], p. 144-147.
- Dans son texte Zhui Shu, d'après (en) John J. O'Connor et Edmund F. Robertson, « Zu Chongzhi », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne [archive])..
- (en) C. Boyer, A History of Mathematics, Wiley, p. 202.
- (en) George E. Andrews, Richard Askey (en) et Ranjan Roy, Special Functions, Cambridge University Press, (ISBN 978-0-521-78988-2), p. 58.
- (en) R. C. Gupta, On the remainder term in the Madhava-Leibniz’s series, vol. 14, t. 1-4, Ganita Bharati, , p. 68-71.
- (en) Charles Hutton, Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms…, London, Rivington, (lire en ligne [archive]), p. 13.
- (en) John J. O'Connor et Edmund F. Robertson, « A chronology of Pi », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne [archive])..
- Citation originale : « I am ashamed to tell you to how many figures I carried these computations, having no other business at the time. »
- (en) Florian Cajori, A History of Mathematical Notations [détail des éditions], volume 2, p. 8-13 nos 395 - 398, accessible en ligne [archive].
- La notation n'est pas utilisée exclusivement, et de plus à des variantes près pour noter le rapport, voir Cajori, ouvrage cité.
- Rien n’indique si c’est sous l’influence de celui-ci ou de son propre chef, cf. Cajori.
- On la trouve par exemple dans Les Éléments de géométrie de Legendre, un ouvrage plutôt destiné à un public scolaire, paru en 1794 ; cf. Cajori.
- « An {ENIAC} Determination of pi and e to more than 2000 Decimal Places », Mathematical Tables and Other Aids to Computation, 4 (29), p. 11–15. (janvier 1950).
- « Statistical Treatment of Values of First 2,000 Decimal Digits of e and of pi Calculated on the ENIAC », Mathematical Tables and Other Aids to Computation, 4 (30), p. 109–111, avril 1950.
- (en) « The constant π: Ramanujan type formulas » [archive].
- (en) Richard Brent, Multiple-precision zero-finding methods and the complexity of elementary function evaluation, New York, Analytic Computational Complexity, (lire en ligne [archive]), p. 151-176.
- La Recherche, no 392, décembre 2005, « L’indispensable nombre π », p. ?[réf. incomplète].
- (en) Lennart Berggren, Jonathan M. Borwein et Peter B. Borwein, Pi: A Source Book, Springer, , 3e éd. (ISBN 978-0-38720571-7, lire en ligne [archive]).
- (en) Bailey, Borwein et Plouffe, « On the Rapid Computation of Various Polylogarithmic Constants », Mathematics of Computation, (lire en ligne [archive] [PDF]).
- (en) Fabrice Bellard, « A new formula to compute the nth binary digit of pi » [archive].
- (en) Simon Plouffe, « Indentities inspired by Ramanujan’s Notebooks (part 2) » [archive] [PDF].
- (en) Alexander J. Yee et Shigeru Kondo, 5 Trillion Digits of Pi [archive].
- (en) « y-cruncher » [archive], sur www.numberworld.org, (consulté le 9 mars 2015)
- (en) Richard Feynman, The Feynman Lectures on Physics, vol. I, , chap. 22 (« Algebra »), p. 10.
- attribuée souvent à Leibniz, mais découverte probablement antérieurement par Gregory, voir (en) John J. O'Connor et Edmund F. Robertson, « A history of Pi », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne [archive]).. Cette formule avait également été trouvée vers 1400 par le mathématicien indien Madhava, mais cette découverte resta inconnue du monde occidental.
- (en) John J. O'Connor et Edmund F. Robertson, « Madhava », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne [archive])..
- (en) Eric W. Weisstein, « Gaussian Integral [archive] », MathWorld.
- (en) Eric W. Weisstein, « Cauchy Distribution [archive] », MathWorld.
- (en) Eric W. Weisstein, « Buffon’s Needle Problem [archive] », MathWorld.
- (en) Alex Bogomolny, « Math Surprises: An Example » [archive], cut-the-knot, (consulté le 28 octobre 2007).
- (en) J. F. Ramaley, « Buffon’s Noodle (en) Problem », Amer. Math. Month., .
- (en) « The Monte Carlo algorithm/method », sur datastructures, .
- (en) Eric W. Weisstein, « Pi Formulas [archive] », MathWorld.
- (en) Xavier Gourdon, « Collection of approximations for π » [archive], Numbers, constants and computation (consulté le 8 novembre 2007).
- ChronoMath http://serge.mehl.free.fr/chrono/Ramanujan.html [archive]
- La constante standard
java.lang.Math.PIprédéfinie en double précision en langage Java [archive]. - Suite A001203 de l'OEIS.
- Formule de Brouncker.
- Fraction découverte par (en) L. J. Lange, « An Elegant Continued Fraction for π », Amer. Math. Month., vol. 106, no 5, , p. 456-458 (JSTOR 2589152). Se déduit en fait d'une série de Nilakantha, par la formule de fraction continue d'Euler.
- Par évaluation en 1 d'un développement de arctan.
- Par transformation du produit de Wallis : Eymard et Lafon 2004, p. 71.
- Voir par ex. Berggren, Borwein et Borwein 2004.
- Par ex. (en) MSNBC, Man recites pi from memory to 83,431 places [archive], 3 juillet 2005, Matt Schudel, Obituaries: "John W. Wrench, Jr.: Mathematician Had a Taste for Pi", The Washington Post, 25 mars 2009, p. B5.
- (en) The Big Question: How close have we come to knowing the precise value of pi? [archive] The Independent, 8 janvier 2010.
- (en) Pi, a mathematical story that would take 49,000 years to tell [archive].
- Voir par exemple Le secret de la grande pyramide de Georges Barbarin.
- Selon The Journal of the Society for the Study of Egyptian Antiquities, (ISSN 0383-9753), 1978, vol. 8, no 4, « la valeur de π apparaissant dans la relation entre la hauteur et la longueur de la pyramide est vraisemblablement co-accidentelle ».
- (en) David Blatner, « 3.14 and the rest » [archive], BBC News Magazine, .
- (en) Tomoko Otake, « How can anyone remember 100,000 numbers? », The Japan Times, (lire en ligne [archive]).
- (en) « Pi World Ranking List » [archive] (consulté le 27 octobre 2007).
- (en) « Chinese student breaks Guiness record by reciting 67,890 digits of pi », News Guangdong, (lire en ligne [archive]).
- (ru) Профессор Андрей Слюсарчук установил мировой рекорд по возможностям человеческой памяти [archive].
- Publié pour la première fois par the academy[Quoi ?], d’après la Revue scientifique, 1905 [archive][réf. incomplète]. Les quatre premiers vers sont connus en 1846, dans Le livre des singularites, Gabriel Peignot, G. P. Philomneste [archive].
- Pi - Supplément au Petit Archimède no 64-65, mai 1980, p. 273.
- Le mot orbe est du masculin mais ce ne fut pas toujours le cas, ceci induit à présent une faute d’accord à « calculée » que l’on peut remplacer par « escompté », par exemple, pour conserver le bon nombre de lettres.
- (en) Yicong Liu, « Oh my, memorizing so many digits of pi » [archive], Silver Chips Online, .
- (en) A. Raz, M. G. Packard, G. M. Alexander, J.T. Buhle, H. Zhu, S. Yu et B. S. Peterson, « A slice of pi : An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist », Neurocase, vol. 15, no 5, , p. 361-372 (DOI 10.1080/13554790902776896) PMID 19585350 [archive].
Liens externes
- La preuve par Lambert de l’irrationalité de π (1761), commentée sur le site Bibnum
- Nombreuses informations historiques et mathématiques sur pi dans pi314.net
- (en) Eric W. Weisstein, « Pi Formulas », MathWorld
- Les décimales de pi, sur images des Maths
- J.-C. Michel, « Le nombre Pi », sur gecif.net






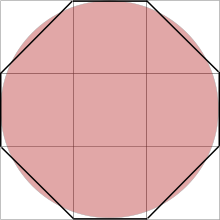


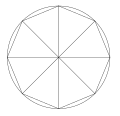




 (
(



Aucun commentaire